Ένα από τα ίσως δυσκολότερα κεφάλαια των μαθηματικών είναι τα ολοκληρώματα. Έχεις όμως ποτέ αναρωτηθεί, γιατί; Τι τα κάνει τόσο δύσκολα; Μήπως δεν αντιλαμβανόμαστε την πραγματική τους αξία και δεν δίνουμε την απαραίτηση προσοχή; Αν και εσύ νιώθεις έτσι, στο άρθρο αυτό θα σε βοηθήσω να βάλεις την σκέψη σου σε μια σειρά.
Στα επόμενα λεπτά, θα προσπαθήσω να σου δώσω μια εντελώς διαφορετική αντίληψη του τι είναι και που χρησιμοποιούνται τα ολοκληρώματα στα μαθηματικά μέσα από παραδείγματα εφαρμογής στην ρομποτική. Θα τα ορίσουμε, με απλό τρόπο και θα αναφέρουμε παραδείγματα χρήσης. Μέσα από τα οποία, θα καταλάβεις την πραγματική τους αξία και πως τα ολοκληρώματα στα μαθηματικά συνδέονται με την εκπαιδευτική ρομποτική.
Ας πάρουμε τα πράγματα από την αρχή.
Το πρόβλημα της μετακίνησης
Ας συμφωνήσουμε οτι για έναν άνθρωπο, είναι απαραίτητο να αντιλαμβάνεται την θέση του στον κόσμο. Το ίδιο σημαντικό είναι και για ένα ρομποτικό σύστημα. Πρέπει με κάποιον τρόπο να γνωρίζει που βρίσκεται. Αλλιώς δεν δεν μπορεί να μετακινηθεί.
Πολλά project εκπαιδευτικής ρομποτικής εστιάζουν στο να μετακινηθεί ένα ρομπότ σε κάποιο σημείο. Αυτό απαιτεί αντίληψη του που βρίσκεται τώρα και που θέλει να πάει. Χωρίς αυτές τις πληροφορίες καμία μετακίνηση δεν είναι εφικτή.
Αυτό που λοιπόν θέλω να κρατήσεις μέχρι εδώ, είναι οτι υπάρχει η τωρινή θέση (που βρίσκεσαι τώρα), η επιθυμητή θέση (που θέλεις να πας) και κάπως, πρέπει να δημιουργηθεί ένα εργαλείο για την μετακίνηση αυτή.
Η λύση στο πρόβλημα της μετακίνησης
Το GPS (Global Positioning System) είναι ένα εργαλείο που χρησιμοποιείται για να γνωρίζουμε την θέση μας. Είναι το μοναδικό εργαλείο; Φυσικά και όχι, απλά βολέυει πολύ, πάρα πολύ! Πάντα; Τι γίνεται σε μια κατάσταση που δεν έχουμε σήμα από τον δορυφόρο όπως σε ένα τούνελ ή μέσα στην θάλασσα; Πως μπορείς να ξέρεις πόσα μέτρα έχεις κινηθεί;
Η λύση σε αυτό το πρόβλημα δεν είναι μία.
Στην ρομποτική, για να μπορούμε να έχουμε την αίσθηση του περιβάλλοντος και να πάρουμε αποφάσεις, χρησιμοποιούμε διάφορους αισθητήρες, όπως:
- επιταχυνσιόμετρο για την επιτάχυνση του οχήματος
- GPS για την θέση του οχήματος
- ταχύμετρο για την ταχύτητα του οχήματος.
Σήμερα, ανάλογα τις παραμέτρους, υπάρχουν διάφορες λύσεις όπως το GPS, wheel encoders κ.α. Όμως, σκέψου τι συμβαίνει σε ένα τούνελ. Σκέψου τι συμβαίνει εκτός του βαρυτικού πεδίου της γης. Εκεί το GPS δεν μπορεί να λειτουργήσει. Χρειαζόμαστε λοιπόν, άλλους τρόπους υπολογισμού της θέσης.
Αυτό ήταν μια εισαγωγή για τα ολοκληρώματα και πως αυτά, μπορούν να προσφέρουν τις πληροφορίες που χρειαζόμαστε.
Θέση και ταχύτητα οχήματος
Η θέση αφορά τα Χ, Υ και Ζ όπως τα αναφέραμε παραπάνω και η ταχύτητα τον ρυθμό μεταβολής της θέσης, δηλαδή πόσο γρήγορα ένα αντικείμενο μεταφέρεται από το σημείο Α στο σημείο Β σε ένα συγκεκριμένο χρονικό διάστημα.
Για παράδειγμα, η μεταφορά ενός οχήματος από Αθήνα στην Πάτρα με 100km/h σημαίνει οτι το όχημα διανύει 100km σε 1 ώρα.
Υπάρχουν περιπτώσεις όπου δεν μπορούμε να έχουμε σήμα με το GPS και για να ξέρουμε την θέση πρέπει να βασιστούμε σε διάφορες άλλες μεθόδους, όπως η ολοκλήρωση της ταχύτητας. Ολοκληρώνοντας την ταχύτητα, έχουμε την θέση του ρομπότ.
Υπολογισμός θέσης βάση της ταχύτητας
Γνωρίζουμε οτι υπάρχει μια σχέση ανάμεσα στην θέση του οχήματος κια στην ταχύτητα του. Μια απλοποιημένη εκδοχή της σχέσης είναι η ακόλουθη:
Η ταχύτητα (υ) είναι ανάλογη της θέσης (x) σε σχέση με τον χρόνο (t). Μια πιο ολοκληρωμένη εκδοχή της σχέσης είναι με χρήση των μεταβολών δηλαδή:
- du η μεταβολή της ταχύτητας
- dx η μεταβολή της θέσης
- dt η μεταβολή του χρόνου
Σε αυτή την περίπτωση, ισχύει οτι η μεταβολή της ταχύτητας (dt) είναι ανάλογη με την μεταβολή της θέσης (dx) στην σχετική μεταβολή του χρόνου (dt).
Ο υπολογισμός της θέσης ή καλύτερα της μεταβολής της θέσης, γίνεται πολύ απλά, λύνοντας την παραπάνω σχέση ως προς dx.
Σε αυτό το σημείο, κάνοντας μια απλή παραδοχή, το όχημά μας να έχει σταθερή ταχύτητα μπορούμε να υπολογίσουμε την θέση του οχήματος, γνωρίζοντας μόνο και μόνο την ταχύτητά του.
Υπενθυμίζω, πως έχουμε υποθέσει οτι το όχημά μας διαθέτει ένα ταχύμετρο που μετρά και μας τροφοδοτεί με την πραγματική του ταχύτητα κάθε στιγμή.
Ας μελετήσουμε ένα παράδειγμα, για το πως θα υπολογίζαμε την θέση ενός οχήματος με σταθερή ταχύτητα.
Περίπτωση με σταθερή ταχύτητα
Έχοντας σταθερή ταχύτητα (υ), μπορούμε να λύσουμε το πρόβλημά του υπολογισμού της θέσης (x) του οχήματος. Ας μελετήσουμε αυτή τη περίπτωση, μέσα από ένα παράδειγμα.
Έστω ένα όχημα που κινείται με ταχύτητα υ=10m/s. Πόσο διάστημα, έχει διανύσει μέσα σε t=10s;
Αν και υπάρχει η σχετική μαθηματική φόρμουλα, ως άνθρωποι είμαστε οπτικά όντα. Πάμε λοιπόν να σχεδιάσουμε και να μελετήσουμε το γράφημα της ταχύτητας – χρόνου. Στον κάθετο άξονα, αποτυπώνουμε την ταχύτητα, σταθερή στα 10m/s και στον οριζόντιο το χρονικό διάστημα 10s.

Η μελέτη του γραφήματος ταχύτητας – χρόνου, μας επιτρέπει να εξάγουμε ένα φανταστικό συμπέρασμα. Οτι ο υπολογισμός της μεταβολής της θέσης του οχήματος (dx), αυτό δηλαδή που ψάχνουμε, γίνεται απλά, υπολογίζοντας το εμβαδό του διαγράμματος ταχύτητας – χρόνου.
Το εμβαδό ενός ορθογωνίου με πλευρές a και b, υπολογίζεται από την σχέση:
Άρα λοιπόν, για να υπολογίζουμε το dx δηλαδή το εμβαδό, πρέπει απλά να πολλαπλασιάσουμε τον dυ και το dt όπως στην παρακάτω σχέση. Σου θυμίζει κάτι;
Αν τοποθετήσουμε και τους αριθμούς, έχουμε την παρακάτω σχέση:
Let’ s recap a bit.
Τι έχουμε καταφέρει; Δεδομένου, οτι η ταχύτητα του οχήματος είναι σταθερή, υπολογίσαμε την θέση του οχήματος, απλά υπολογίζοντας το εμβαδό του γραφήματος ταχύτητας – χρόνου.
Υπάρχει όμως ένα πρόβλημα!
Η υπόθεση που έχουμε κάνει είναι εσφαλμένη. Κανένα αυτοκίνητο δεν κινείται με απολύτως σταθερή ταχύτητα και κυρίως κανένα αυτοκίνητο δεν μπορεί να ξεκινήσει με 100m/s. Χρειάζεται τουλάχιστον 2 sec για να επιταχύνει (ναι ακόμη και τα TESLA)
Το πρόβλημα στον υπολογισμό
Στη πραγματικότητα ένα γράφημα ταχύτητας – χρόνου είναι σαν το παρακάτω:
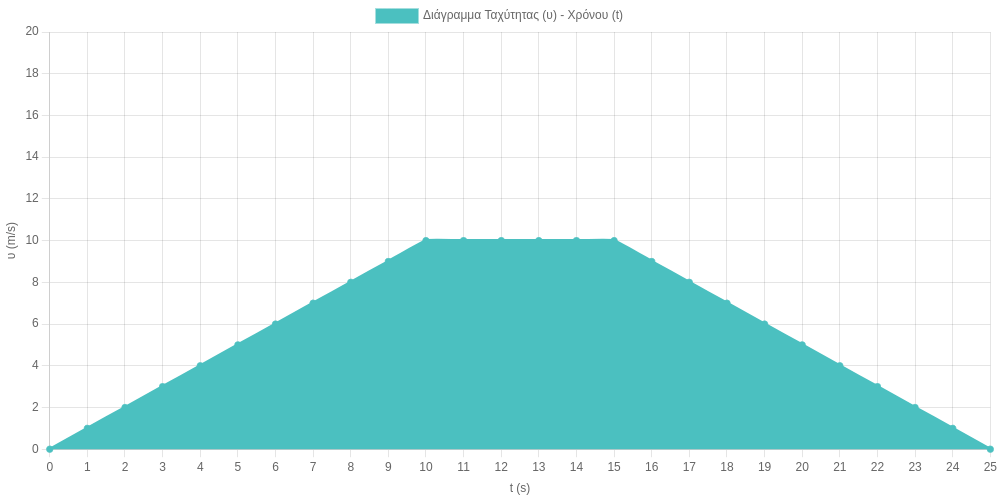
Στα πρώτα 10s υπάρχει μια διαδικασία επιτάχυνσης από 0m/s στα 10m/s, έπειτα έχουμε σταθερή ταχύτητα για ένα διάστημα 6sec και έπειτα, ακολουθεί ένα διάστημα επιβράδυνσης για 10s μέχρι η ταχύηττα να επανέλθει πίσω στα 0m/s.
Το πραγματικό πρόβλημα σε αυτή τη περίπτωση είναι πως πλέον δεν μπορούμε να υπολογίσουμε την θέση με τον ίδιο τρόπο καθώς το σχήμα δεν είναι ορθογώνιο. Ναι, υπάρχουν τύποι για υπολογισμό εμβαδού τραπεζίου. Ας τραβήξουμε όπως λίγο ακόμη το σκοινί, σε κάτι πιο ρεαλιστικό.
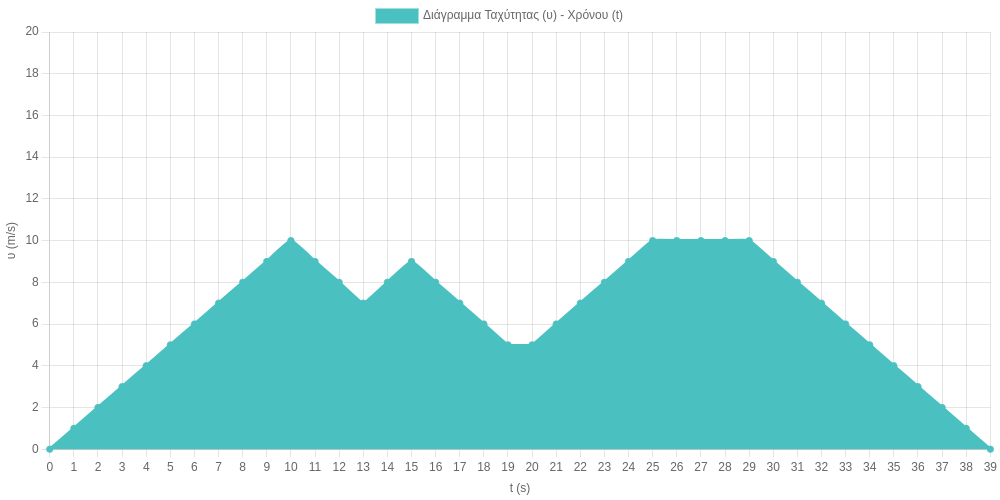
Στο παραπάνω σχήμα, μπορείς να υπολογίσεις το εμβαδό που αντιστοιχεί και στον υπολογισμό της θέση του ρομποτικού οχήματος; Ίσως να μπορέσεις, αλλά θεωρώ πως πλέον είναι αντιληπτό, οτι στην πραγματική ζωή, τα “σχήματα” που δημιουργούνται είναι πολύ πιο πολύπλοκα.
Αυτός είναι και ο λόγος που χρειάζομαστε τα τα ολοκληρώματα για να τον υπολογισμό της θέσης ενός οχήματος.
Περίπτωση με δυναμική ταχύτητα
Μια προσέγγιση όταν υπάρχει δυσκολία στον υπολογισμό, είναι η μελέτη μια συγκεκριμένης περιοχής. Ψάχνουμε την απόσταση που έχει διανύσει το όχημα για διάστημα 10s. Ας δούμε πρώτα, αν μπορούμε να υπολογίσουμε την απόσταση, που έχει διανύσει το όχημα για διάστημα 1sec.
Σε αυτό το διάστημα του χρόνου, ορίζουμε δύο χρονικές στιγμές t0 και t1 (μεταγενέστερη του t0). Η ταχύτητα του οχήματος την t0 στιγμή είναι υ0 και η ταχύτητα του οχήματος την t1 στιγμή υ1. Έτσι μπορούμε να υπολογίσουμε την μεταβολή της θέσης dx ως:
Συνεπώς, στο διάστημα χρόνου από 0sec μεχρι και 1sec, το αυτοκίνητο κινήθηκε dx. Αντίστοιχα, μπορούμε να κάνουμε τον υπολογισμό για το διάστημα από 1sec μέχρι και 2sec αλλά και από 2sec μέχρι και 3sec κ.τ.λ.
Πόσο μεγάλα θα είναι τα διαστήματα χρόνου; Είναι πάντα 1sec το σωστό dt για να “σπάσουμε” το συνολικό χρονικό διάστημα; Η απάντηση είναι πως όχι και γι αυτό, χρησιμοποιούμε τα ολοκληρώματα.
Αντί να κάνουμε το παραπάνω άθροισμα σε όλα τα dx που υπολογίζουμε, μπορούμε να υπολογίσουμε την ταχύτητα ως το ολοκλήρωμα της θέσης.




